数据分析必须懂的假设检验
来源:引流技巧
编辑:引流技巧
时间:2025-10-04

数据分析屠龙技:假设检验与AB测试。
 假设检验,也就是大名鼎鼎的AB Testing。俗话说得好,再优秀的产品经理也跑不过一半AB测试。
抽样
数据分析中,虽然数据越多越齐越好,可是受限于各类因素的制约,我们并不能获取全部的数据。比如Excel的性能限制,比如数据库不支持大文件导出、或者是无法全量进行的用户调研等。
抽样是一种应对方法,通过样本来推断总体,抽样结果提供的仅仅是相应总体特征的估计,「估计」这一点很重要。
抽样有很多方式,样本首要满足随机性。比如进行社会访谈,你不能只选择商场人流区,因为采访到的人群明显是同一类人群,反而会遗漏郊区和乡镇的人群,遗漏宅男,遗漏老人。
互联网产品中,抽样也无处不在,大名鼎鼎的AB测试就是一种抽样,选取一部分人群验证运营策略或者产品改进。通常筛选用户ID末尾的数字,比如末尾选择0~4,于是抽样出了50%的用户,这既能保证随机性,也能保证控制性。
毕竟抽样的目的是验证和检验,需要始终保证用户群体的完全隔离,不能用户一会看到老界面,一会看到改进后的新界面。以上也适用于推荐算法的冠军挑战,用户分群等。
至于放回抽样,分层抽样,在互联网的数据分析中用不太到,这里就略过了。
点估计
既然我们已经知道如何选择一个样本,接下来需要从样本推断总体。
列举一个场景。产品和运营人员每周都会进行一次用户调研,调研随机抽取30位用户对产品进行打分,分数0~10。根据历史数据计算出平均7.5分,标准差为1分。
现在的问题是,用户调研能否反应一些产品的状况?比如发布新版本,或者做了营销活动后,怎么判断是正面影响还是负面?假设本月产品经理们发布了一次新版本,这次调研抽取30位用户平均评分是7.3,究竟是正常的波动还是做糟糕了?
在统计学中,把总体的平均值标准差等称为总体参数,把样本的种种指标称为点估计量。s是样本标准差,σ是总体标准差。n是样本,N是总体。
点估计在原有的符号上加横线表示,比如样本均值,念做x拔(打出这个字符麻烦,我简称为拔了)。
x拔是样本均值,现实中不可能保证每次调研的数据都是一致的,假设将抽样过程一而再,再而三的进行下去,那么调研获得的平均分也是波动的。此时,样本均值x拔是一个随机变量,称它的概率分布为x拔的抽样分布。
每次抽样得出的不同均值,必然会有一个期望值,E(x拔) = u,E(x拔)就是所有大量抽样的可能值的均值。对简单随机抽样,我们可以认为其数学期望等于u总体均值。当点估计量的期望值等于总体参数时,称为无偏估计。
当样本量占总体5%以上时,有求样本标准差公式如下:
假设检验,也就是大名鼎鼎的AB Testing。俗话说得好,再优秀的产品经理也跑不过一半AB测试。
抽样
数据分析中,虽然数据越多越齐越好,可是受限于各类因素的制约,我们并不能获取全部的数据。比如Excel的性能限制,比如数据库不支持大文件导出、或者是无法全量进行的用户调研等。
抽样是一种应对方法,通过样本来推断总体,抽样结果提供的仅仅是相应总体特征的估计,「估计」这一点很重要。
抽样有很多方式,样本首要满足随机性。比如进行社会访谈,你不能只选择商场人流区,因为采访到的人群明显是同一类人群,反而会遗漏郊区和乡镇的人群,遗漏宅男,遗漏老人。
互联网产品中,抽样也无处不在,大名鼎鼎的AB测试就是一种抽样,选取一部分人群验证运营策略或者产品改进。通常筛选用户ID末尾的数字,比如末尾选择0~4,于是抽样出了50%的用户,这既能保证随机性,也能保证控制性。
毕竟抽样的目的是验证和检验,需要始终保证用户群体的完全隔离,不能用户一会看到老界面,一会看到改进后的新界面。以上也适用于推荐算法的冠军挑战,用户分群等。
至于放回抽样,分层抽样,在互联网的数据分析中用不太到,这里就略过了。
点估计
既然我们已经知道如何选择一个样本,接下来需要从样本推断总体。
列举一个场景。产品和运营人员每周都会进行一次用户调研,调研随机抽取30位用户对产品进行打分,分数0~10。根据历史数据计算出平均7.5分,标准差为1分。
现在的问题是,用户调研能否反应一些产品的状况?比如发布新版本,或者做了营销活动后,怎么判断是正面影响还是负面?假设本月产品经理们发布了一次新版本,这次调研抽取30位用户平均评分是7.3,究竟是正常的波动还是做糟糕了?
在统计学中,把总体的平均值标准差等称为总体参数,把样本的种种指标称为点估计量。s是样本标准差,σ是总体标准差。n是样本,N是总体。
点估计在原有的符号上加横线表示,比如样本均值,念做x拔(打出这个字符麻烦,我简称为拔了)。
x拔是样本均值,现实中不可能保证每次调研的数据都是一致的,假设将抽样过程一而再,再而三的进行下去,那么调研获得的平均分也是波动的。此时,样本均值x拔是一个随机变量,称它的概率分布为x拔的抽样分布。
每次抽样得出的不同均值,必然会有一个期望值,E(x拔) = u,E(x拔)就是所有大量抽样的可能值的均值。对简单随机抽样,我们可以认为其数学期望等于u总体均值。当点估计量的期望值等于总体参数时,称为无偏估计。
当样本量占总体5%以上时,有求样本标准差公式如下:

 假设检验,也就是大名鼎鼎的AB Testing。俗话说得好,再优秀的产品经理也跑不过一半AB测试。
抽样
数据分析中,虽然数据越多越齐越好,可是受限于各类因素的制约,我们并不能获取全部的数据。比如Excel的性能限制,比如数据库不支持大文件导出、或者是无法全量进行的用户调研等。
抽样是一种应对方法,通过样本来推断总体,抽样结果提供的仅仅是相应总体特征的估计,「估计」这一点很重要。
抽样有很多方式,样本首要满足随机性。比如进行社会访谈,你不能只选择商场人流区,因为采访到的人群明显是同一类人群,反而会遗漏郊区和乡镇的人群,遗漏宅男,遗漏老人。
互联网产品中,抽样也无处不在,大名鼎鼎的AB测试就是一种抽样,选取一部分人群验证运营策略或者产品改进。通常筛选用户ID末尾的数字,比如末尾选择0~4,于是抽样出了50%的用户,这既能保证随机性,也能保证控制性。
毕竟抽样的目的是验证和检验,需要始终保证用户群体的完全隔离,不能用户一会看到老界面,一会看到改进后的新界面。以上也适用于推荐算法的冠军挑战,用户分群等。
至于放回抽样,分层抽样,在互联网的数据分析中用不太到,这里就略过了。
点估计
既然我们已经知道如何选择一个样本,接下来需要从样本推断总体。
列举一个场景。产品和运营人员每周都会进行一次用户调研,调研随机抽取30位用户对产品进行打分,分数0~10。根据历史数据计算出平均7.5分,标准差为1分。
现在的问题是,用户调研能否反应一些产品的状况?比如发布新版本,或者做了营销活动后,怎么判断是正面影响还是负面?假设本月产品经理们发布了一次新版本,这次调研抽取30位用户平均评分是7.3,究竟是正常的波动还是做糟糕了?
在统计学中,把总体的平均值标准差等称为总体参数,把样本的种种指标称为点估计量。s是样本标准差,σ是总体标准差。n是样本,N是总体。
点估计在原有的符号上加横线表示,比如样本均值,念做x拔(打出这个字符麻烦,我简称为拔了)。
x拔是样本均值,现实中不可能保证每次调研的数据都是一致的,假设将抽样过程一而再,再而三的进行下去,那么调研获得的平均分也是波动的。此时,样本均值x拔是一个随机变量,称它的概率分布为x拔的抽样分布。
每次抽样得出的不同均值,必然会有一个期望值,E(x拔) = u,E(x拔)就是所有大量抽样的可能值的均值。对简单随机抽样,我们可以认为其数学期望等于u总体均值。当点估计量的期望值等于总体参数时,称为无偏估计。
当样本量占总体5%以上时,有求样本标准差公式如下:
假设检验,也就是大名鼎鼎的AB Testing。俗话说得好,再优秀的产品经理也跑不过一半AB测试。
抽样
数据分析中,虽然数据越多越齐越好,可是受限于各类因素的制约,我们并不能获取全部的数据。比如Excel的性能限制,比如数据库不支持大文件导出、或者是无法全量进行的用户调研等。
抽样是一种应对方法,通过样本来推断总体,抽样结果提供的仅仅是相应总体特征的估计,「估计」这一点很重要。
抽样有很多方式,样本首要满足随机性。比如进行社会访谈,你不能只选择商场人流区,因为采访到的人群明显是同一类人群,反而会遗漏郊区和乡镇的人群,遗漏宅男,遗漏老人。
互联网产品中,抽样也无处不在,大名鼎鼎的AB测试就是一种抽样,选取一部分人群验证运营策略或者产品改进。通常筛选用户ID末尾的数字,比如末尾选择0~4,于是抽样出了50%的用户,这既能保证随机性,也能保证控制性。
毕竟抽样的目的是验证和检验,需要始终保证用户群体的完全隔离,不能用户一会看到老界面,一会看到改进后的新界面。以上也适用于推荐算法的冠军挑战,用户分群等。
至于放回抽样,分层抽样,在互联网的数据分析中用不太到,这里就略过了。
点估计
既然我们已经知道如何选择一个样本,接下来需要从样本推断总体。
列举一个场景。产品和运营人员每周都会进行一次用户调研,调研随机抽取30位用户对产品进行打分,分数0~10。根据历史数据计算出平均7.5分,标准差为1分。
现在的问题是,用户调研能否反应一些产品的状况?比如发布新版本,或者做了营销活动后,怎么判断是正面影响还是负面?假设本月产品经理们发布了一次新版本,这次调研抽取30位用户平均评分是7.3,究竟是正常的波动还是做糟糕了?
在统计学中,把总体的平均值标准差等称为总体参数,把样本的种种指标称为点估计量。s是样本标准差,σ是总体标准差。n是样本,N是总体。
点估计在原有的符号上加横线表示,比如样本均值,念做x拔(打出这个字符麻烦,我简称为拔了)。
x拔是样本均值,现实中不可能保证每次调研的数据都是一致的,假设将抽样过程一而再,再而三的进行下去,那么调研获得的平均分也是波动的。此时,样本均值x拔是一个随机变量,称它的概率分布为x拔的抽样分布。
每次抽样得出的不同均值,必然会有一个期望值,E(x拔) = u,E(x拔)就是所有大量抽样的可能值的均值。对简单随机抽样,我们可以认为其数学期望等于u总体均值。当点估计量的期望值等于总体参数时,称为无偏估计。
当样本量占总体5%以上时,有求样本标准差公式如下:
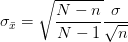

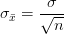

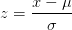

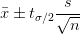

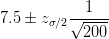

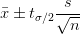

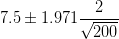




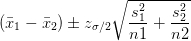



相关文章:
相关推荐:
栏目分类

最新文章

热门文章


